Research Projects
Estimating temperature and precipitation uncertainties with quantile neural networks
The climate system is highly chaotic and unpredictable. As a result, a significant portion of climate science research focuses on constraining climate uncertainties under changing conditions. In light of these uncertainties, we propose a data-driven probabilistic technique, a type of quantile neural network, for quantifying uncertainties that requires few assumptions and has a straightforward implementation. Using a synthetic dataset, we demonstrate the advantages of this quantile neural network over field-standard baselines that make stronger assumptions, such as linear relationships between inputs and outputs and normally distributed uncertainties. We then apply this technique to weather station temperature data and satellite observations of precipitation, finding that daily maximum temperatures are well described by nonlinear relationships with normally distributed uncertainties, whereas precipitation depends significantly nonlinearly on the model inputs and exhibits non-normal statistics. This work shows how quantile neural networks can be easily implemented to gain a more accurate representation of uncertainties in the geosciences.
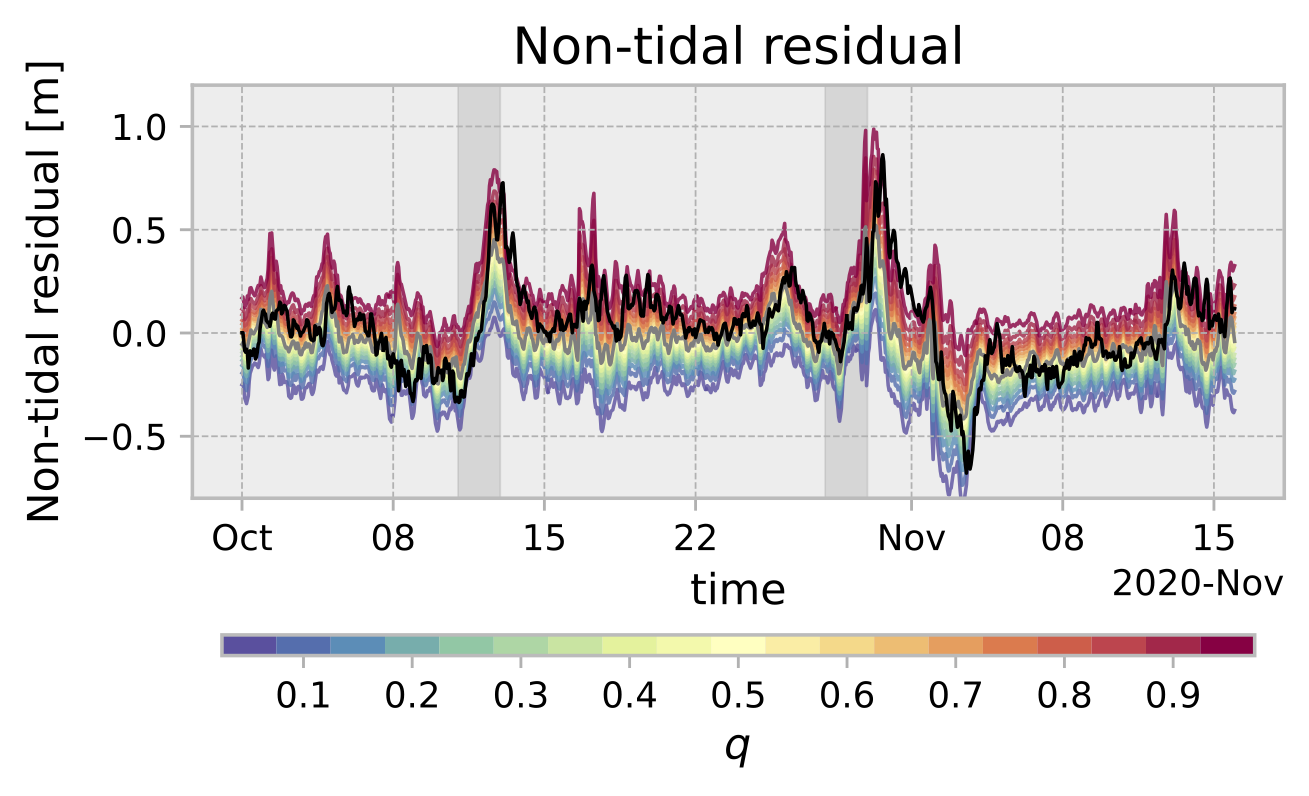
Learning efficient forecasts for regional sea surface height dynamics
Sea surface height forecasts are impacted by many different sources of uncertainty due to the highly nonlinear and chaotic dynamics of the climate system. Thus, many different approaches are commonly taken to develop forecasts, ranging from coupled-model physics simulations to data-driven approaches trained on observational products. Over the past few decades, Linear Inverse Modeling (LIM) has become an eminent statistical technique for building forecasts in the climate sciences, at times producing forecasts that can outperform numerical simulations. However, it assumes that the modeled system is described by linear dynamics, an often strong assumption for the chaotic and complex climate system.
In this study, we leverage the theory of non-linear dynamical systems (Koopman operator theory) to develop better forecasts than LIM. We train a Convolutional Neural Network (CNN) autoencoder with a dynamical propagator in the latent space (a “Koopman Autoencoder”) to produce regional sea surface height forecasts. This approach exploits both practical and theoretical limitations of LIM. First, learning the timestepping and dimensionality reduction simultaneously results in better forecasts than with LIM, where dimensionality reduction and propagation are learned sequentially. Thus, the dimensionality reduction is performed in a way that is explicitly advantageous for forecasting. Second, our CNN autoencoder transforms the representation of high-dimensional, nonlinear dynamics into a low-dimensional latent space with linearized dynamics. This makes our model more interpretable. The Koopman autoencoder results in forecast performance gains of 5-10% over linear inverse models using models of similar complexity.
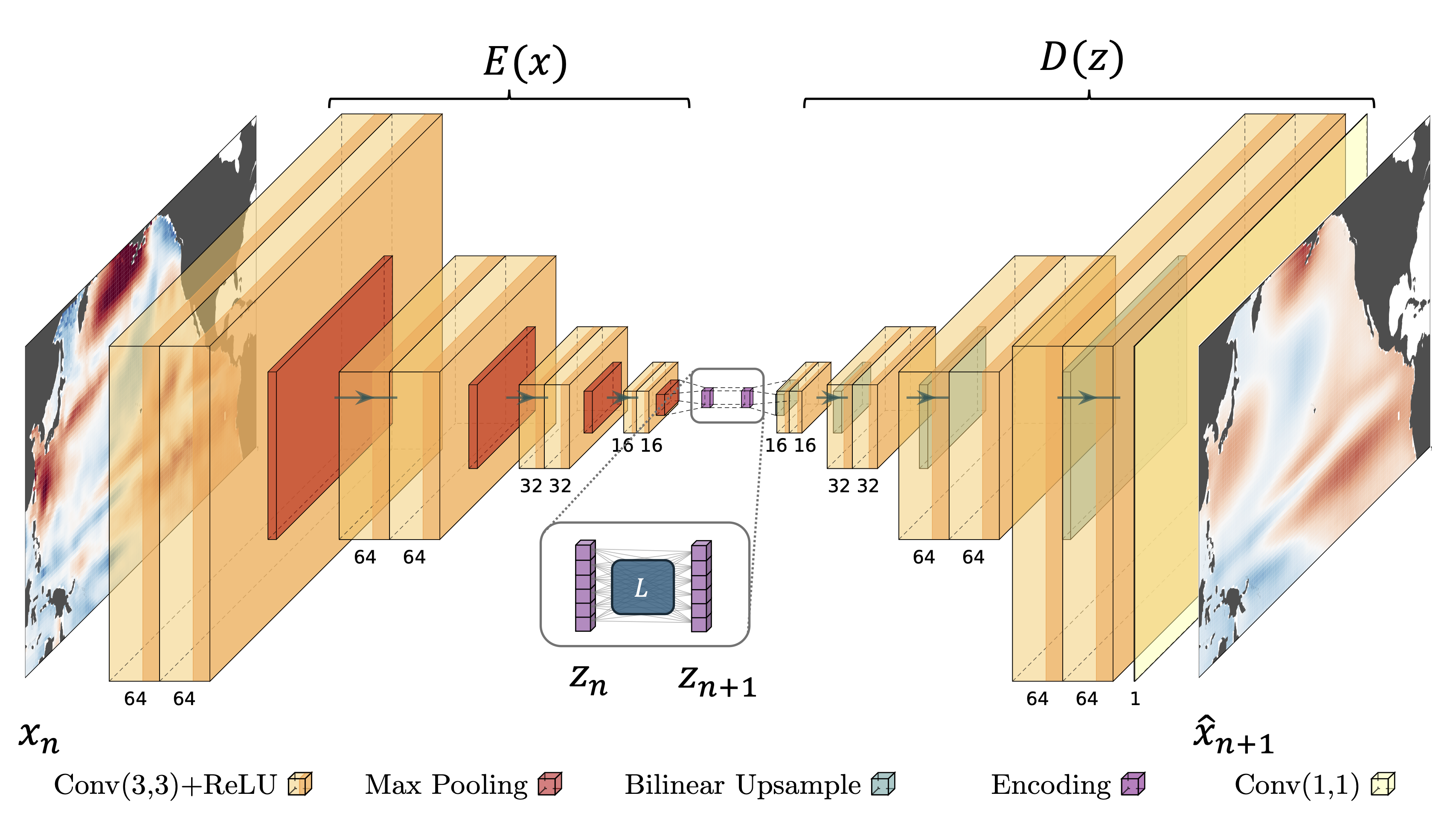
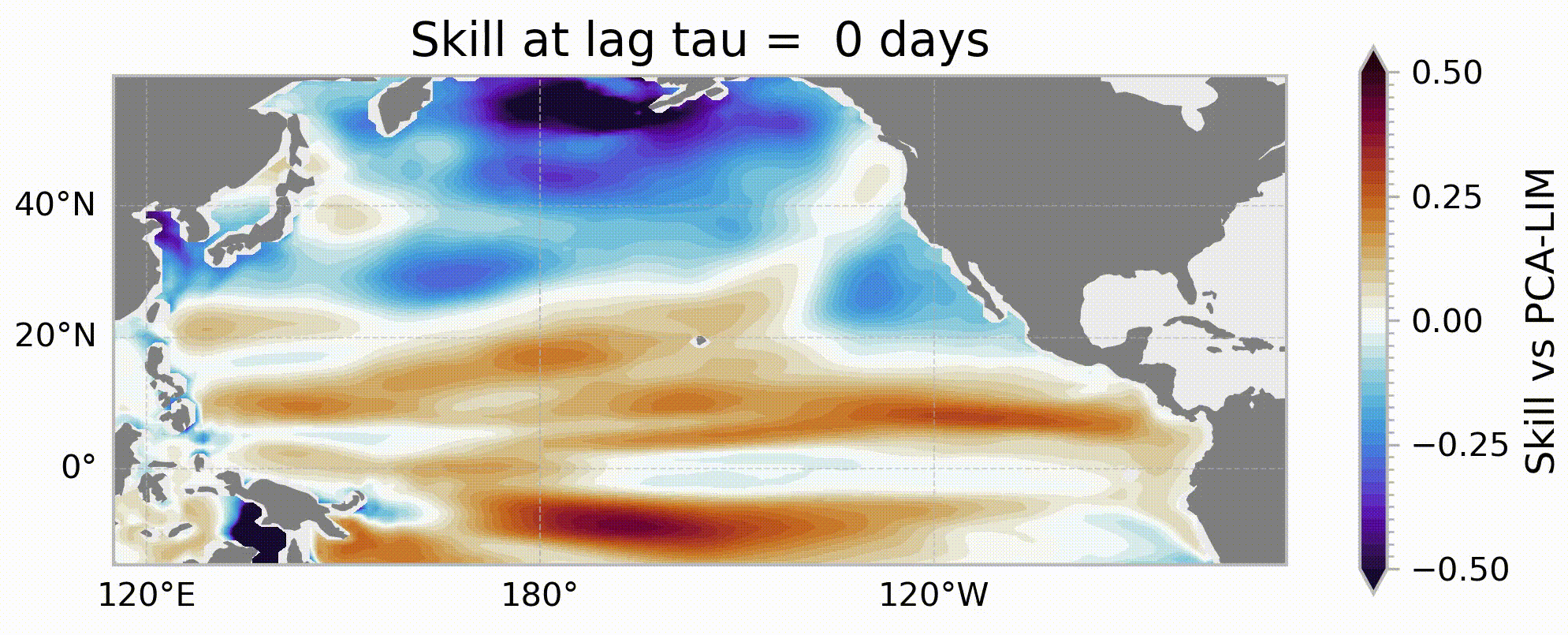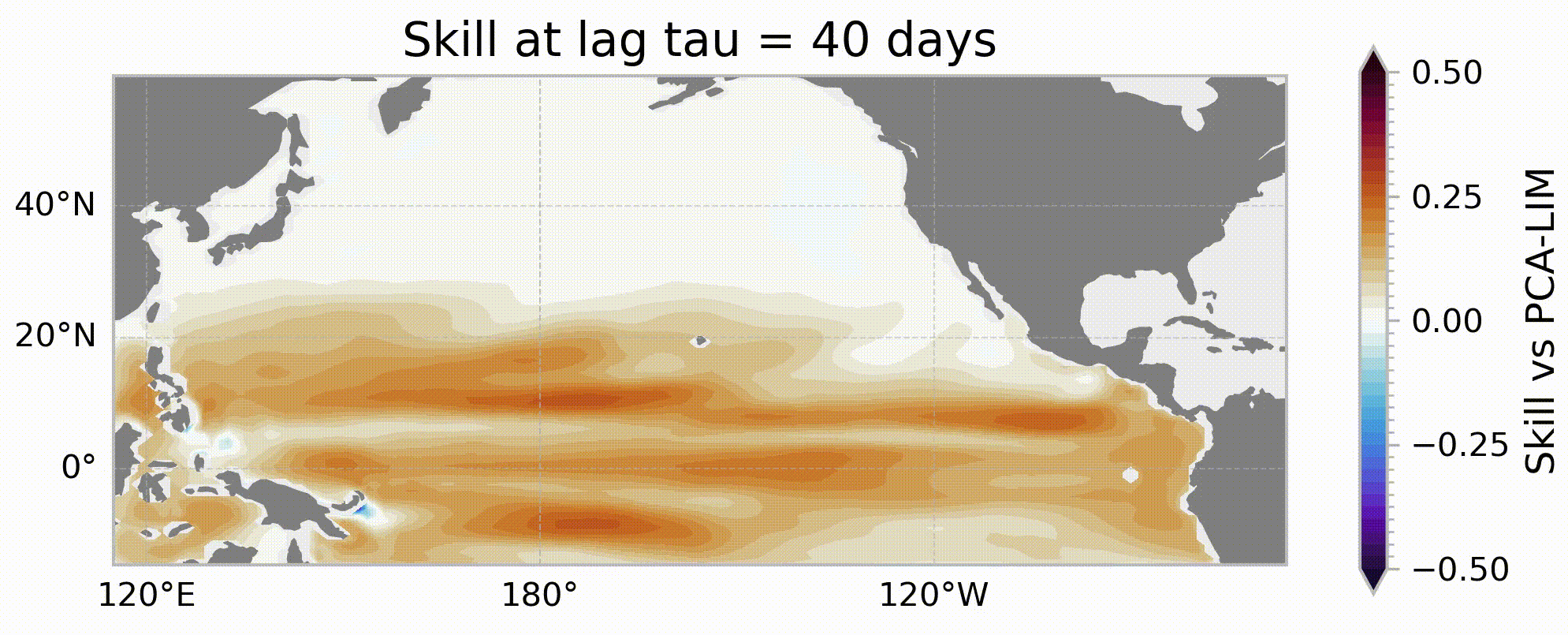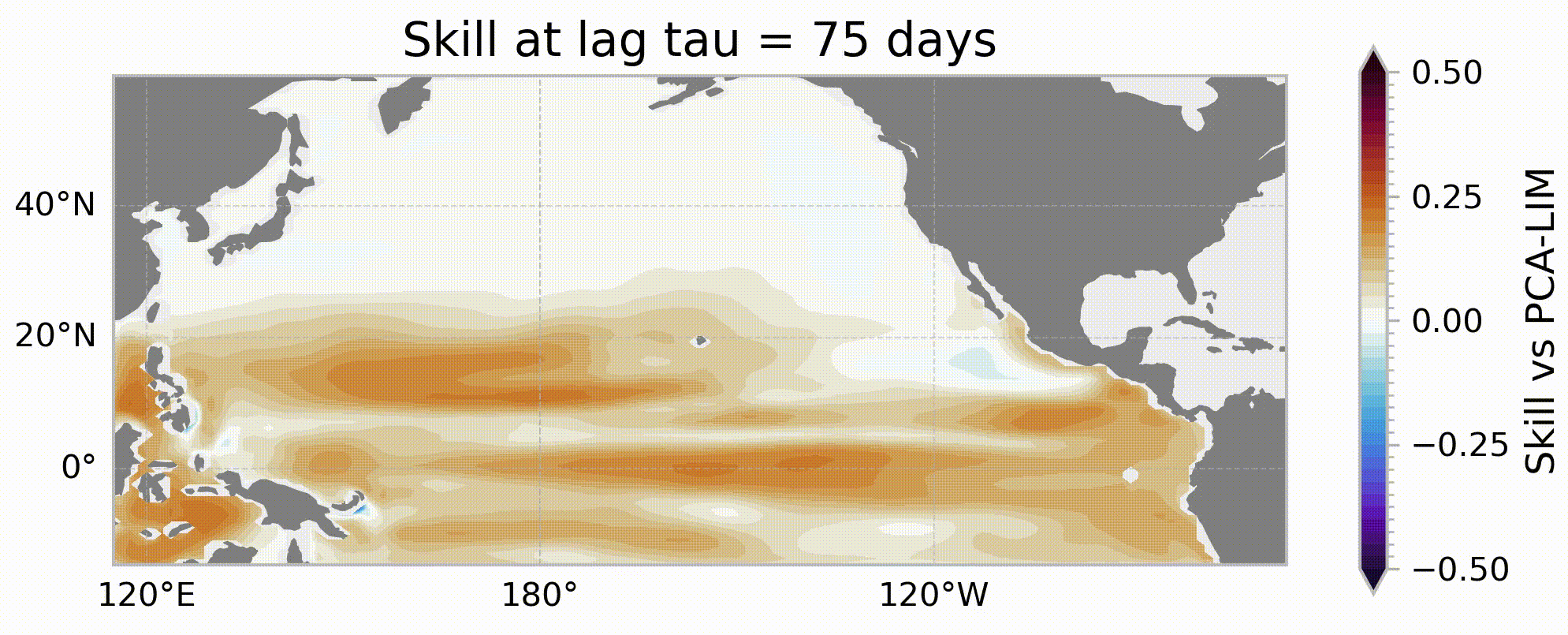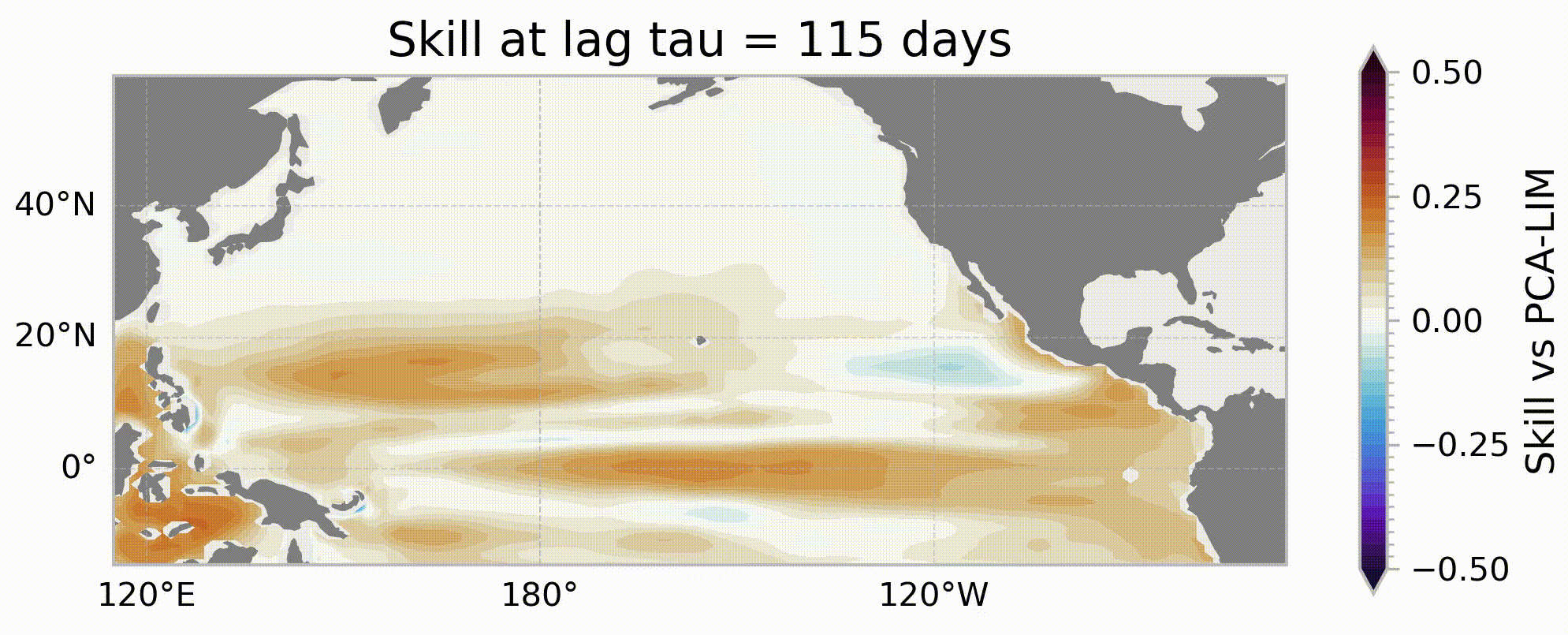
Identifying sources of sea level predictability using uncertainty permitting machine learning with explainable AI
Reliable sea level forecasts on daily-to-seasonal timescales (1–180 days) are hindered by numerous sources of uncertainty from both the atmosphere and ocean. This time horizon is notoriously challenging for forecasting, as predictability from the atmosphere is lost but longer-term sources of predictability from the ocean have yet to emerge. Nevertheless, the daily-to-seasonal time horizon is critical for municipalities to mitigate potential damages from high-tide tide flooding.
One approach to improving forecasts on this time horizon is to focus on intial conditions which can extend predictability horizons. Identifying these initial conditions which are inherently more predictable can allow forecasts to be made on time horizons that would not normally be considered. In this study, we leverage mean-variance estimation networks to identify state-dependent sources of predictability for sea level using the Community Earth System Model (CESM2) Large Ensemble dataset (LENS2). Using these uncertainty-quantifying neural networks and interpretable machine learning procedures (Explainable AI), we examine how the dominant drivers of predictability change over a range of different forecast leads at a variety of locations. For instance, while local persistence drives dynamic sea level predictability at Guam (14°N, 145°E) on shorter forecast lead times, as the forecast lead is extended to seasonal timescales, propagating Rossby waves emerge as a dominant source of predictability. This study shows how uncertainty-quantifying machine learning can be used to help identify sources of predictability on a range of forecasting leads and could help improve forecasts crucial to administrators.
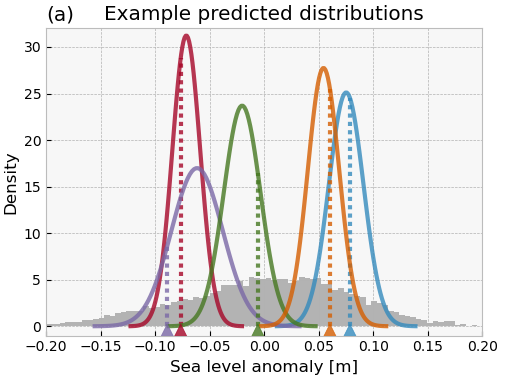
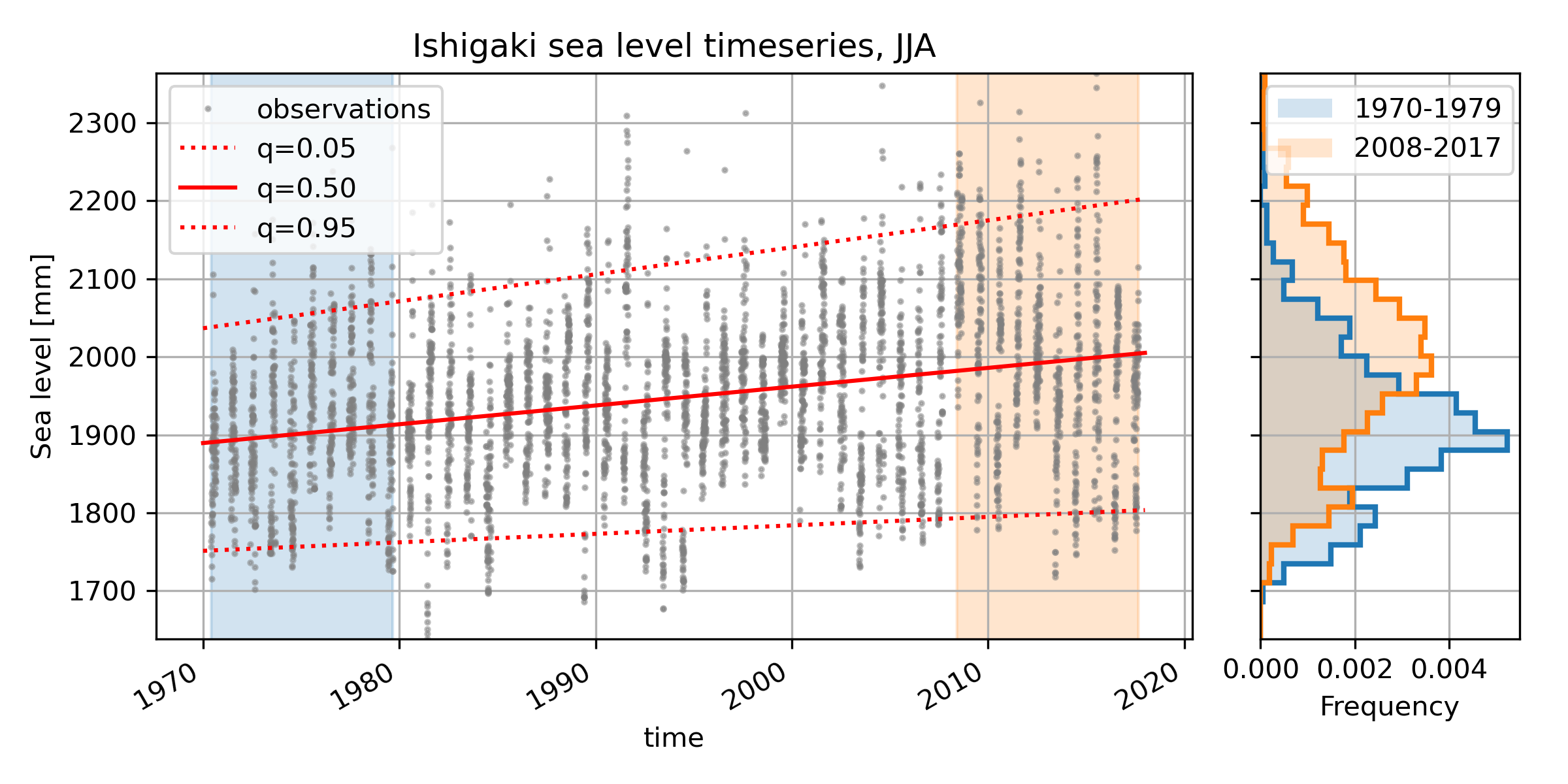
Exploring the nonstationarity of sea level probability distributions
Changes in the shape of the probability distribution of geophysical variables can significantly impact the occurrence of extremes. Therefore, understanding and quantifying these changes is paramount to understanding changing risks under rising seas. In this collaboration, we propose a theoretical framework for quantifying changes in probability distributions, modifying an approach by McKinnon and Rhines (2016) to improve interpretability.